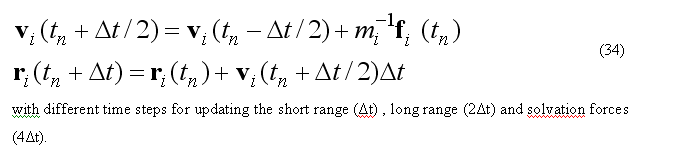
See "Instalation and RUN" topic.
Main Program file : MDynSBmain.f
Start from the call of the input parameters
1. call inputMDSApar
reads the main Input file
filenam = './MdynPar.inp' ! in current job_dir
the file has the fixed name and located in the current job directory
the main input file MdynPar.inp defines main parameters of the job (see chapter input file description)
2. call initMolecTopSeq01
reads a defined molecular PDB file, which can be defined in the MdynPar.inp file
or has the standard name ./molec.pdb and located in the current job directory ./ ;
defines residue sequence
3. call initMolecTopSeq02
calculates 12neighbour list (covalent bonds connecting atoms) using a predefined topology
information about resdues stored in the $MDSBHOME/dat
the pair12 list array: pair12List(*) is the basic molecular topology information.
Based on the pair12List(*) the all other lists are calculated, namely
Bonded triplets and quartets to form list of covalent angles, torsion angles, improper torsion angles.
The list of triplets and quartets are calculated via tree algorithm
Call vbondListPDB2(atomXYZ,
& natom,atomNumb,atomName,resName,chName,resNumb,
& nres,resNameRes,chNameRes,
& atomNameEx,startAtInRes,
& nmoveatom,moveAtomList,
& pair12List,startPairL12,nPairL12,np12MAX,
& pair13List,startPairL13,nPairL13,np13MAX,
& pair14List,startPairL14,nPairL14,np14MAX,
& bond12List,nbond12,
& trip123List,nTrip123,np123MAX,
& quar1234List,nQuar1234,np1234MAX,
& quarImp1234L,nImp1234,nImp1234MAX)
the call of the subroutine initMolecTopPDB results in the complete definition of the molecular topology
from the input molec.pdb 3D structure.
4. call initFFieldParam
Initialization of the force field parameters for the bond, angle, torsion angle, improper angle deformations,
van der waals non bond interactions and atomic point charges for the electrostatic interactions.
For bond, angle, torsion and improper angles a respective list of parameters are generated and stored in the arrays.
A list All force field parameters are based on the amber94 force field parameter set [Cornell et.al 1995].
Molecular mechanical energy is based on the standard equations for the force field of second generation
amber94 [Cornell et.al 1995].
Decoding of the atom names (residue names) to the forceField atom name is based on the look up table
ffAtomTypeFile = $MDSBHOME/dat/atmAAmberff.dat
5. Extraction of the data from Library file
All search of the proper names in the look up table of the MDynSB program are based on
the hashing of a records in the look up table, i.e. conversion of the table in numerically
sequential order. If several records of the look up table have the same hash number (degenerated case),
they are placed in a linkedLis for this hash number.
Force field parameters are taken from the file:
ffParFile = $MDSBHOME/dat/bsparBATV.dat
code fragment to initialize force field parameters
c get ff-atom code from atomNames
call defFFatomName (ffAtomTypeFile,
& natom,atomNameEx,ResName,chName,
& ffAtomName,atomQ)
c
c define bondDef parameters for pair12List()
c
call getBondDefPar(ffParFile,
& natom,atomNameEx,ResName,chName,ffAtomName,
& bond12List,nbond12,bond12ParL)
c c define valence angles def parameters
call getVangDefPar(ffParFile,
& natom,atomNameEx,ResName,chName,ffAtomName,
& trip123List,nTrip123,ang123ParL)
c define Improper angle def parameters
call getImpDefPar(ffParFile,
& natom,atomNameEx,ResName,chName,ffAtomName,
& quarImp1234L,nImp1234,impAng1234ParL)
c define torsion parameters
call getTorsPar(ffParFile,
& natom,atomNameEx,ResName,chName,ffAtomName,
& quar1234List,nQuar1234,quar1234ParL,quar1234nPar)
c
c assign atomMass and vdwParameters
call getVDWatMass(ffParFile,
& natom,atomNameEx,ResName,chName,ffAtomName,
& nVDWtype,atomVDWtype,atomVDW12ab,atomMass)
c
c all FField Parameters are defined
6. call initSolvatGSmod
Defines atomic parameters of the current structure for the Gaussian Shell implicit solvation model [Lazaridis, 1999].
A parameters of the GS model are stored in the files:
solvGSPar_aa_amb.dat
solvGSPar.dat
7. call initMDStart(tempT0)
Initialize MD calculation:
Calculate the Initial nonBondPair lists
c generate three nonbonded atom pair Lists: van der Waals, Coulombic and solvation model.
c
makeVdW = 1
makeCL = 1
makeSL = 1
c
call initNonBondList(atomXYZ,makeVdW,makeCL,makeSL)
c
Calculates the forces on atoms for initial atomic coordinates
initial forces on atoms
c
fcall = 0
call initAllForce(fcall,atomXYZ,makeVdW,makeCL,makeSL,
& eVbondDef,vbdefForce,
& eVangDef,vAngdefForce,
& eImpDef,impDefForce,
& eTorsDef,torsAngForce,
& engVDWR1,vdwForceR1,
& engCOULR1,coulForceR1,
& engCOULR2,coulForceR2,
& restr1Eng,restr1AtForce,
& molSolEn, atomSolEn,atomSolFr)
c
Calculates initial atomic velocities, which are distributed according to Maxwell law
probability(vi) = ( ) exp(-mivi2/kT)
c
call initVelocity(temp,natom,
& nmoveatom,moveAtomList,atomMass,atomVel0)
c
8. Run MD
The subroutine mdRun perform MD run for a given number of time steps ntimeMX
c
call mdRun(ntimeMX,ntime0,ntime,ntimeR1,ntimeR2,
& ntimeF1,ntimeF2,ntimeF3,deltat,
& tempTg,tauTRF,atype,optra,wtra,nwtra,cltra)
c
9. Simulated Annealing optimization
c
call simAnnealing(nSAstep,SAProtcol)
c
with user defined SAProtocol(nstep,T) consisted of nSAstep.
Each step of the SA is MD run of nstep with particular temperature T.
All atoms of the molecular system consists of two sets of fixed
and moving atoms.
The force are calculated only for the moving atom set.
For covalent bond deformation we use the GROMOS functional form
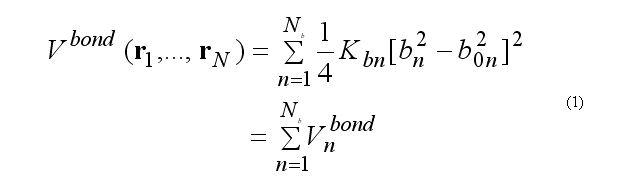
where
rij = ri - rj
bn = rij .
This functional form is equivalent to the usual harmonic function for a small deformations but a computationally is more effective.
Force on atom i due to bond n
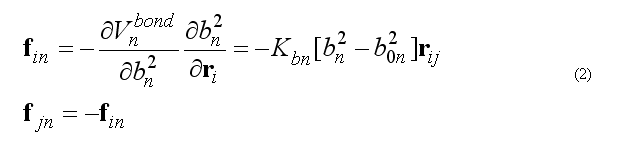
Total bond deformation force on atom i is the sum over all bonds n involving the atom i.
The calculation of the force fin is doing by
subroutine vbonddefenf(xyz1,xyz2,bondPar,edef,f1,f2) (see file vdefenforce.f)
The covalent angle deformation energy function has the form
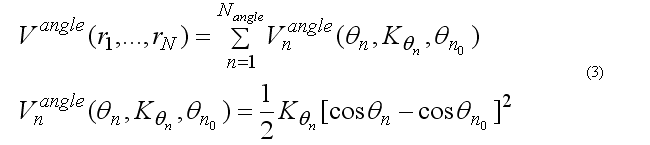
This functional form is equivalent to the usual harmonic function for the angles for a small angle deformation but a computationally is more effective. The angle 2n ( at the j ) is between atoms i-j-k . The cosine of the angle 2n

The forces on atoms i,j,k due to the deformation of the angle 2n
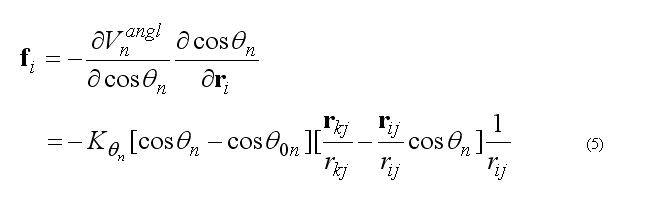
respectively force on atom k
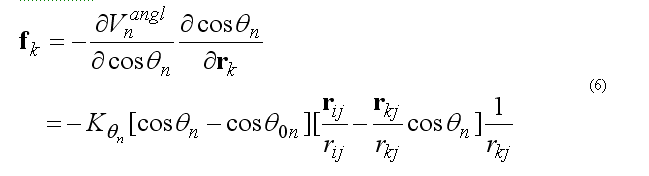
force on atom j is given from the conservation of the total force acting on three atoms

The covalent angle deformation energy and force are calculated in subroutine
subroutine vangldefenf(xyz1,xyz2,xyz3,angPar,
& edef,f1,f2,f3)
(see file vdefenforce.f)
The total torsion energy is a sum over a set of torsion angles for the four atoms i-j-k-l with a rotation around bond j-k ,
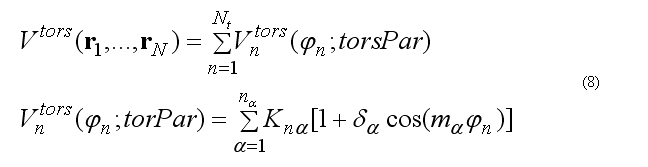
where torsion energy for bond j-k can have several torsion barriers with different multiplicity.
Torsion angle N is defined as
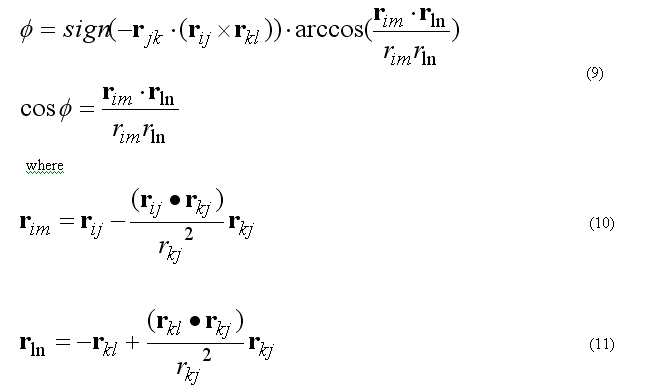
The forces on atoms i,j,k,l due to the single term of eq.(8b) are

The torsion energy and force are calculated via
subroutine torsanglenf(xyz1,xyz2,xyz3,xyz4,nTorsH,
& torsPar,eTors,f1,f2,f3,f4)
c torsPar(4*nTorsH) = {pass,Vt/2/pass,cos(delta),nFi },…
c eTors = sum{ Ki*[1+cos(delti)cos(i*Ftors)] }; i=1,..,nTorsH
c
Torsion parameters are taken from the LibData = bsparBATV.dat
The extraction of the torsion parameters from LibData = bsparBATV.dat for all quartets is done by
subroutine getTorsPar(ffParFile,
& natom,atomNameEx,ResName,chName,ffAtomName,
& quar1234L,nQuar1234,quar1234Par,quar1234nPar)
c
c InPut:
c ffParFile - ffParameters file
c natom,atomNameEx,ResName,chName : PDB info
c ffAtomName(ia) - FFatomName to search table
c the quar1234L(i),i=1,..,nQuar1234 : the QuartetList
c RESULT: quar1234Par(16*nQuar1234) - torsionFF parameters for list
c of quartets
c pass,Vt/2,delta,nFi - (printed) for each torsHarmonics,
c pass,Vt/2/pass,cos(delta),nFi - finally in array
c 4- torsionHarmanics is possible.
c quar1234nPar(iQuart) - number of torsHarmonics for the torsAngl
c
The improper torsion angle deformation keeps the four atoms 1-2-3-4 (i-j-k-l ) in specified geometry. The first atom in the improper quartet is a planar or (tetrahedral) atom. For example atoms Ci-CAi-N(i+1)-Oi are kept planar. The out of plane potential
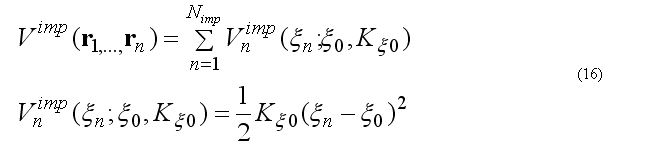
CA-N-C-CB are kept in the tetrahedral configuration (L-amino acid) or CA-C-N-CB (D-amino acid) if CA in the united atom (CH) presentation.
The out of plane angle is defined for j-i-k four atoms with i is the planar (tetrahedral)
L
angle between to planes (i-j-k) and (j-k-l) with rotation angle around j-k, other words the
torsion angle in the sequence i-j-k-l
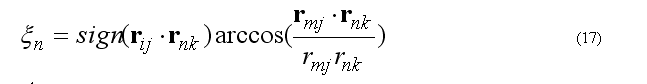
where

The forces on atoms i,j,kl due to a single term Vn
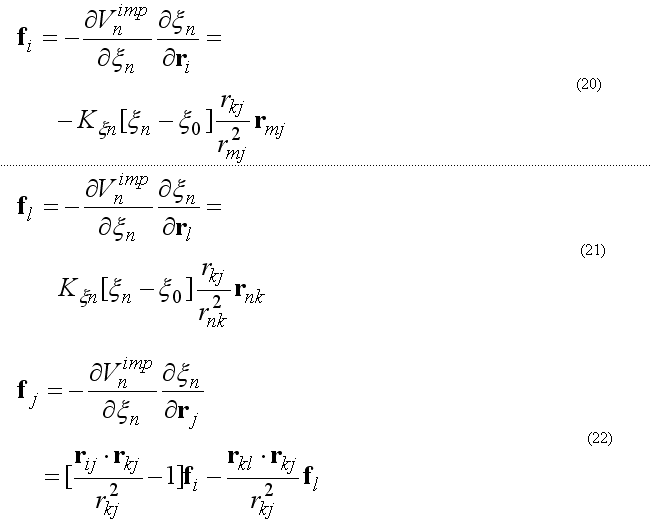
finally from the third Newton law
The improper energy and forces for a given improper quartet of atoms are calculated by the subroutine
c improper torsion energy force
c
subroutine imprtorsanglenf(xyz1,xyz2,xyz3,xyz4,impPar,
& eImpt,f1,f2,f3,f4)
c
c ImptPar(2) = K1, ksi0
All valence back-bond deformation are calculated in the file initAllForce.f
subroutine initAllForce(fcall,atomXYZ,
& makeVdWs,makeCLs,makeSLs,
& eVbondDef,vbdefForce,
& eVangDef,vAngdefForce,
& eImpDef,impDefForce,
& eTorsDef,torsAngForce,
& engVDWR1,vdwForceR1,
& engCOULR1,coulForceR1,
& engCOULR2,coulForceR2,
& restr1Eng,restr1AtForce,
& molSolEn, atomSolEn, atomSolFr)
c
include 'xyzPDBsize.h'
include 'xyzPDBinfo.h'
include 'pair1234array.h'
include 'nbondPairVCS.h'
include 'vdw12Par.h'
include 'restrainInfo.h'
include 'loopInfo.h'
include 'movingAtom.h'
include 'solvGSarray.h'
include 'optionPar.h'
c
. . . . . . . . . . . . . . . . . . . . .
c
c all GeoDef forces are calculated at each step
call allAtVBondEForce(atomXYZ,
& natom,bond12List,nbond12,bond12ParL,
& eVbondDef,vbdefForce )
c
c
call allAtVangEForce(atomXYZ,
& natom,trip123List,nTrip123,ang123ParL,
& eVangDef,vAngdefForce )
c
c
call allAtImpTEForce(atomXYZ,
& natom,quarImp1234L,nImp1234,impAng1234ParL,
& eImpDef,impDefForce )
c
c torsionEnForces
c
call allAtTorsEForce(atomXYZ,
& natom,quar1234List,nQuar1234,
& quar1234ParL,quar1234nPar,
& eTorsDef,torsAngForce )
c
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
The deformation forces are calculated at each time step in the MD run.
The non bonded pair interactions are calculated for the pair list. Pair list for the central atom i is a sequence of atom numbers for atom within the radius R from the central atom. Three separate pair lists are calculated. The Van der Waals pair list(i) includes atom j if
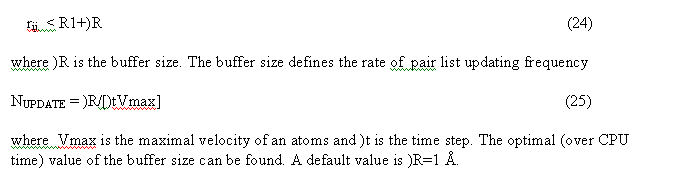
The linked list and all pairList (nnbPairLV, nnbPairLC, nnbPairLS) are calculated in the subroutine
c
subroutine nonbondListVCS(rcutV,rcutC,rcutS,atomXYZ,atomQ,
& rbuffV,rbuffC,rbuffS,
& makeVdW,makeCL,makeS,
& natom,atomNumb,atomName,resName,chName,resNumb,
& nres,resNameRes,chNameRes,
& atomNameEx,startAtInRes,
& nmoveatom,moveAtomList,moveFlag,
& pair12List,startPairL12,nPairL12,
& pair13List,startPairL13,nPairL13,
& pair14List,startPairL14,nPairL14,
& nbpairListV,startnbPairLV,nnbPairLV,nnbpLVMAX,
& nbpairListC,startnbPairLC,nnbPairLC,nnbpLCMAX,
& nbpairListS,startnbPairLS,nnbPairLS,nnbpLSMAX)
c
fragment of code for the linked list calculation:
c distribute atoms over cells
c make linked list of atoms in cells
c headat(n) - head(incellN)
c linkList(ia) - linkedList
ixm=1
iym=1
izm=1
do ia = 1,natom
c calculate cell numb
i3=3*ia-3
xyzi(1)=atomXYZ(i3+1)-xMIN(1)
xyzi(2)=atomXYZ(i3+2)-xMIN(2)
xyzi(3)=atomXYZ(i3+3)-xMIN(3)
ix = xyzi(1)/cellh+1
iy = xyzi(2)/cellh+1
iz = xyzi(3)/cellh+1
if(ixm .lt. ix)ixm = ix
if(iym .lt. iy)iym = iy
if(izm .lt. iz)izm = iz
c cell number
ncell = ix + (iy-1)*nsiz(1) + (iz-1)*nsiz(1)*nsiz(2)
if(ncell .gt. ncell3MAX)then
write(kanalp,*)'ERROR!:nonbondList: ncell3MAX is low !!'
stop
end if!
c make linked list
linkList(ia) = headat(ncell)
headat(ncell) = ia
end do !ia
c end of linked list calculation
The pair lists VDW and COULOMbic energy exclude 12, 13, 14 covalent bonded pairs. The Solvent model pairList
include all 12,13, 14 pairs.
The pair list are calculated for the range respectively:
c
rcutV2 = (rcutV + rbuffV)**2 ! range for List1 -
VDWaals - nbPairListV
rcutV2m = (rcutV - rbuffC)**2 ! range for List2 - Coulombic twin
range - nbPairListC
rcutC2p = (rcutC + rbuffC)**2 ! range for List2
rcutS2 = (rcutS + rbuffS)**2 ! range for SolvationGSList -
nbPairListS
c
see file nonbobdListVCS.f
Van der waals forces are calculated for the non-bonded pair list nbpairListV()for atoms j within rij < RCUTV the cutoff radius for van der waals interactions. The modified potential 6-12 are used
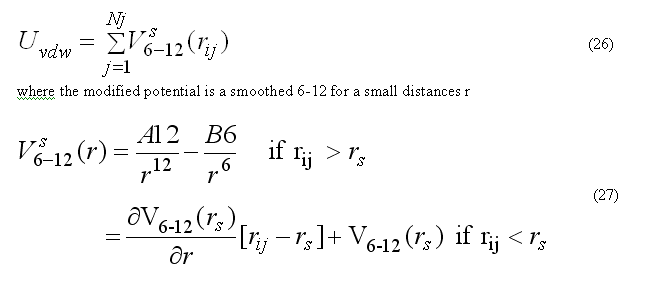
the pair list for atom i includes atoms j > i, to count each pair interaction once. The force Fvdwi on atom i due to interaction with atoms in the pair list
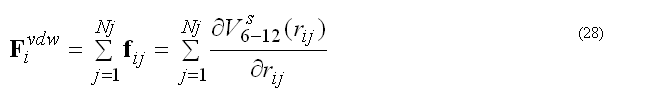
The modified (smoothed) 6-12 potential prevents over-flow when atoms are too close and generates smooth driving forces to resolve clash problems between atoms in molecular dynamics simulations, see
c subroutine vdwenforceij(dij2,dij1,rij,A12,B12,evdw,fi) c
The coulombic energy and forces for atom i are calculated for all pairs within the radius RCUTC.
The coulombic energy/forces for a central atom i are calculated for the classical coulombic law or as a coulombic interaction between two charges on the compensating background charge uniformly distributed within the sphere of radius RCUTC
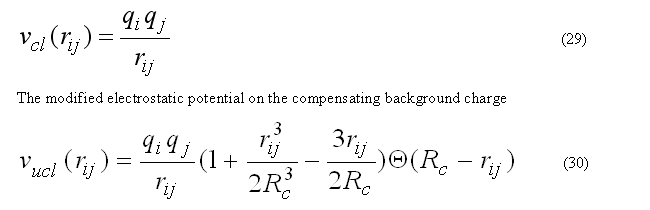
has zero interaction energy and forces for the rij > RCUTC. This form of electrostatic interactions is better suitable to prevent energy conservation in the molecular dynamic calculation, see
c
subroutine coulenforceij(var,rcutC,dij2,dij1,rij,qi,qj,ecoul,fi)
c
The nonbonded energy and force within short range RCUTV=R1 are calculated in the subroutine
c allAtNonBondEForce : VDW and COULOMBIC
c
subroutine allAtVDWEForceR1(atomXYZ,atomQ,
& natom,nmoveatom,moveAtomList,
& nbpairListV,startnbPairLV,nnbPairLV,
& pair14List,startPairL14,nPairL14,
& nVDWtype,atomVDWtype,atomVDW12ab,
& rcutV,rcutC,engVDW,vdwForce,engCOULR1,coulForceR1)
c
for the pair list nbpairListV() and pair14List(). The last one includes all 1-4 neihgbours
for which the amber force field uses the scaling factors for van der waals and coulombic interactions.
To increase performance of the van der waals energy/force calculations the table of
coefficient A12, B12 for all atom types are precalculated and then right values A12/B12 for a given
atom types in the pair ij are extracted from the vdw AB-parameter table
c get pointer to the AB table
call vdw12TablePos(nVDWtype,t1,t2,t12)
p4 = 4*t12
A12 = atomVDW12ab(p4-3)
B12 = atomVDW12ab(p4-2)
c
The long-range electrostatic forces within RCUTV < rij < RCUTC are calculated via the subroutine
c
subroutine allAtVDWEForceR2(atomXYZ,atomQ,
& natom,nmoveatom,moveAtomList,
& nbpairListC,startnbPairLC,nnbPairLC,
& rcutR1,rcutR2,engCOULR2,coulForceR2)
c
c LongRamge - RCUT1 < rij < RCUT2
The program keep separately the short-range and the long-range electrostatic energy and force.
The implicit solvation model - the Gaussian Shell model of Lazaridis & Karplus is used to calculate the solvation energy [POTEINS 35: 133-152, 1999]. The solvation free energy of the atom i
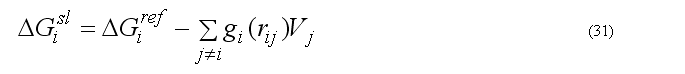
where sum is going over all neighbors of atom i which exclude volume Vj from the solvation volume around of the atom i. The function gi(r) describe the solvation energy density in the volume around the atom i and is approximated by the Gaussian function
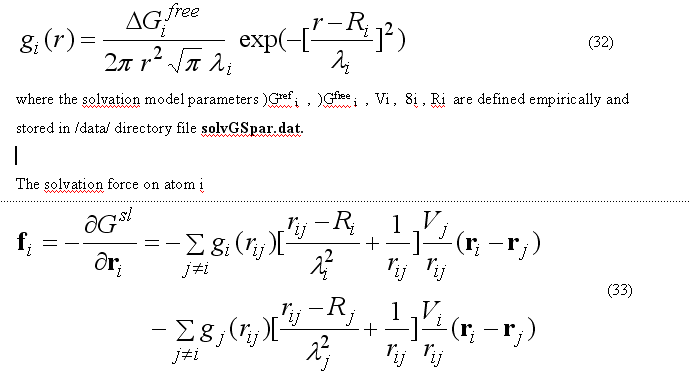
The sum over all solvation forces fi is zero.
The solvation forces are calculated by subroutine
c
call SolventEnForces(natom, atomXYZ,
& atomName,startPairL12,nPairL12,pair12List,
& nbpairListS,startnbPairLS,nnbPairLS,
& atomSolPar, molSolEn, atomSolEn, atomSolFr)
c
An MD run is performed by subroutine
c
subroutine mdRun(ntimeMX,ntime0,ntime,ntimeR1,ntimeR2,
& ntimeF1,ntimeF2,ntimeF3,deltat,
& tempTg,tauTRF,atype,optra,wtra,nwtra,cltra)
c
c MD RUN propagates MDtraj from files in mdAtomXYZvel.h
c [ atomXYZ0(*),atomVel0(*) ]
c call initMDStart(T) inits the MD start
c from the INput atomXYZ(*)-->atom0XYZ(*)
c
c ntimeMX max number of time steps
c ntime0 - executed number of timesteps in the previous call
c ntime executed number of timesteps in this call
c ntimeR1, ntimeR2 - update frequency for R1, R2 pairLists
c ntimeF1,ntimeF2 - update freq for R1=(vdw+coulR1), R2-coulR2 en/forces
c ntimeF3 - SOLVation forces
c GeoEn/force ntimeFg=1 - standart
c deltat- timestep, temp - initial(temp) of MD run
c tempTg - target T for NTV ansemble[K]
c tauTRF - tau Relaxation Factor [ps]
c atype - ansamble type = 0/1 - NEV, NTV
The MD algorithm consist of a long loop over the time steps.
For each time step MD trajectory is propagated for the )t = 1-2 femto sec,
as defined by user.
The pair lists are updated for each n-th timestep equal to ntimeR1, ntimeR2 for the short-range and for the twin-range long-range electrostatic energy calculations.
c
call initNonBondList(atomXYZ0,makeVdW,makeCL,makeSL)
c
The atomic forces due to deformation of covalent structure and short-range non-bonded
calculation are updated for the each ntimeF1-th time step, the long-range
electrostatic are updated for the each ntimeF2-th step and solvation forces are updated for each ntimeF3-th time step.
{Note! In the current version the multiple time
step for pair list update and md equation integration are equal. The general case is not tested !}
c update forces/energy
call initAllForce(fcall,atomXYZ0,doVdWef,doCLef,doSLef,
& eVbondDef,vbdefForce,
& eVangDef,vAngdefForce,
& eImpDef,impDefForce,
& eTorsDef,torsAngForce,
& engVDWR1,vdwForceR1,
& engCOULR1,coulForceR1,
& engCOULR2,coulForceR2,
& restr1Eng,restr1AtForce,
& molSolEn, atomSolEn, atomSolFr)
MD simulation can be done with a specified set of forces. The set of forces can be specified by the array fEngWF(*)
c
eGeoDef = fEngWF(1)*eVbondDef + fEngWF(2)*eVangDef
& + fEngWF(3)*eImpDef + fEngWF(4)*eTorsDef
& + fEngWF(8)* restr1Eng
engCOUL = fEngWF(6)*engCOULR1 + fEngWF(7)*engCOULR2
engPOTENT = eGeoDef + fEngWF(5)*engVDWR1 + engCOUL +
& molSolEn*fEngWF(9)
c
For one time step propagation of the MD trajectory is done by the subroutine
c make mdStep call mdTimeStepProp(nmoveatom,moveAtomList,deltat) c
which uses multi step leap-frog algorithm to calculate velocities and positions at time (t+deltat).
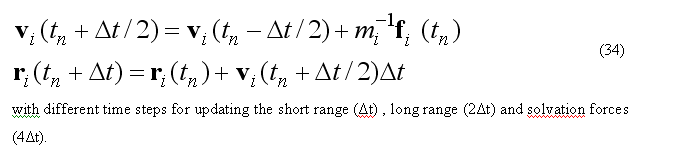
At each time step the temperature control routine performs calculation of the total kinetic energy
of the moving atoms. The relaxation the average temperature of the atomic system
to the specified value are give via the weak-coupling method or Berendsen method,
which scale the velocity by the factor lambTR(t)

Trajectory is written for each nwtra time steps. The trajectory can be written for atomic positions (and for atomic velocietis) in the user specified file.
Method description
Docking method is performed by subroutine runLigDock02 in the mDyn09 program
procedure runLigDock02
perform docking of molecular ligand of size up to ~120 atoms.
The algorithm flow can be described as:
1) Calculation of the accessible surface of the protein. Calculation of a surface grid for probe sphere of radius ~ average atomic radius, and contact positions [bindSiteAt01(*)] with protein atoms. Calculation are done by subroutine surf_SAS04.
2) Calculation of a surface grid points for a probe ligand of radius of typical aromatic
ring [benzene] gridsizeSAS ~ 3.0 A. The surface grid are calculated by clustering of surface
contact positions bindSiteAt01(*) and the surface grid bindGridXYZSAS01(*) is generated. The contact
score [nsasGridPoint(*)] equal to the number of contact atomic positions included in to the surface
grid point bindGridXYZSAS01(*) is calculated.
The bindGridXYZSAS01(*) are sorted by descent of the contact score value
nsasGridPoint(*) and presents an initial trial positions for refined docking of ligand.
3) Refined docking is performed via subroutine runLigDock01(ig,bindGridXYZSAS01loc). For each initial positions bindGridXYZSAS01(*) for ligand center.
The best docking variant for the ligand can be chosen as a file LigDockFinMMM.nnn.pdb with minimal potential energy engPOTENTLG:
Examples
1bty : benzamidine-trypsine complex
File #LigBindGridOnSAS: X Y Z contactScore ATOM 1 LBSt 1 16.536 26.130 8.764 11 ATOM 2 LBSt 2 29.319 14.972 16.378 11 ATOM 3 LBSt 3 6.595 15.454 32.366 9 ATOM 4 LBSt 4 28.049 26.396 3.572 9 ATOM 5 LBSt 5 37.370 14.662 29.278 8 ATOM 6 LBSt 6 9.605 28.662 39.481 7 ATOM 7 LBSt 7 18.280 35.574 15.402 7 ATOM 8 LBSt 8 30.648 34.679 44.060 7 ATOM 9 LBSt 9 34.040 33.767 21.484 7 ATOM 10 LBSt 10 5.056 19.922 18.987 6 ATOM 11 LBSt 11 25.308 5.865 13.437 6 ATOM 12 LBSt 12 13.241 31.812 30.019 6 ATOM 13 LBSt 13 6.174 15.317 15.623 6 ATOM 14 LBSt 14 15.230 11.995 39.322 6 ATOM 15 LBSt 15 42.858 27.966 33.933 6 ATOM 16 LBSt 16 39.046 14.805 5.421 5 ATOM 17 LBSt 17 24.676 37.002 14.221 5 ATOM 18 LBSt 18 39.100 25.116 6.122 5 ATOM 19 LBSt 19 25.156 6.498 5.813 5 ATOM 20 LBSt 20 14.736 13.757 2.279 5 ATOM 21 LBSt 21 35.933 31.703 11.547 5 ATOM 22 LBSt 22 45.035 21.844 22.099 5 ATOM 23 LBSt 23 12.210 8.874 28.161 5 ATOM 24 LBSt 24 11.197 11.080 32.573 5 ATOM 25 LBSt 25 25.549 16.554 -0.897 4 ATOM 26 LBSt 26 34.793 8.348 15.236 4 ATOM 27 LBSt 27 26.857 9.202 21.336 4 ATOM 28 LBSt 28 34.072 12.246 27.335 4 …..
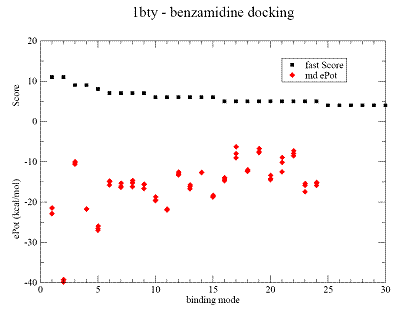
Fig.1. Docking results for benzamidine on trypsine - 1bty complex. |
A - contact Score (black square) for binding grid points vs refined potential energy of ligand binding (red diamonds).
|
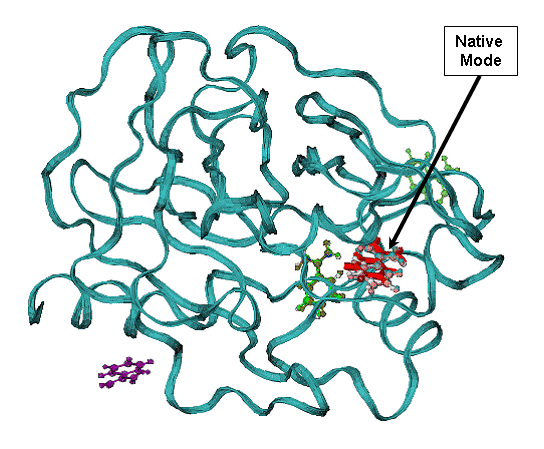
 |
B - minimum energy docking mode (red bonds), RMSD = 0.54 A for all non Hydrogen
atoms ligand of the native binding mode.
CPK- green and violet are less favorable binding modes with low binding energy are shown in (A). CPK (pink) - native binding mode of benzamidine in 1bty. |
|
Fig.2 Docking results for benzamidine on thrombin. |
A - Contact Score (black square) for binding grid points vs refined potential energy of ligand binding (red diamonds).
|
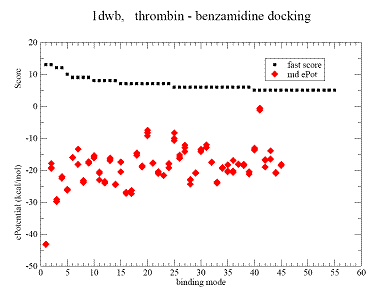 |
B (CPK blue) - minimum energy docking mode. Less favorable binding modes are shown - yellow, brown, green. CPK- (red) native benzamidine binding mode in 1dwb complex,
|
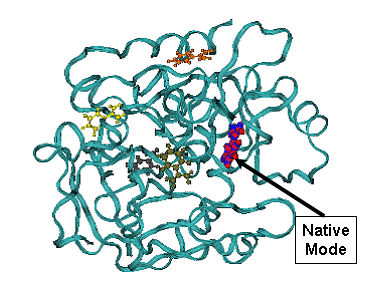
Minimum energy mode has RMSD = 0.27 A from the native binding mode of benzamidine. |
Fig.3. Docking result for biotine on streptavidine , 1stp complex. |
A - contact Score (black square) for binding grid points vs refined potential energy of ligand binding (red diamonds).
|
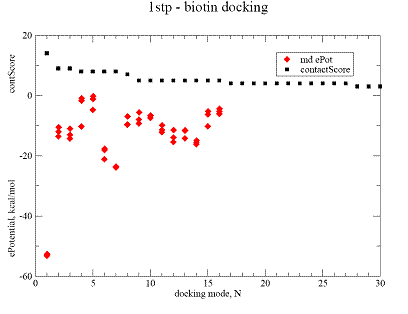 |
B - minimum energy docking mode structure of biotine - CPK, lines - native biotine in the 1stp complex.
|
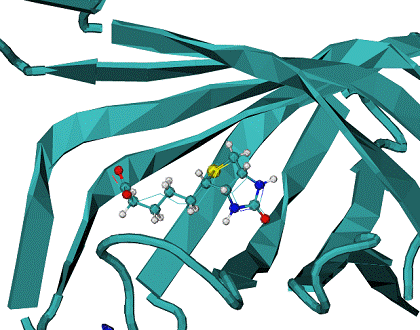
Minimum energy mode has RMSD = 0.96 A from the native binding mode of biotine. |
Fig. 4. Docking result for ILE-VAL dipeptide on Trypsinogen/pancreatic trypsin inhibitor. |
A - contact Score (black square) for binding grid points vs refined potential energy of ligand binding (red diamonds).
|
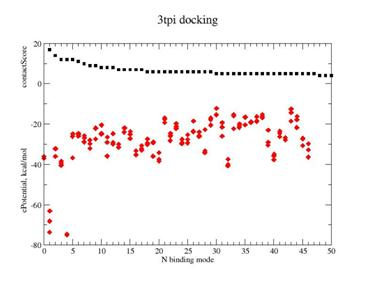 |
B - Lines are minimum energy docking modes of rank 1- 4 structures of ILE-VAL peptide - lines, CPK - native binding mode of biotine in the 1stp complex.
|
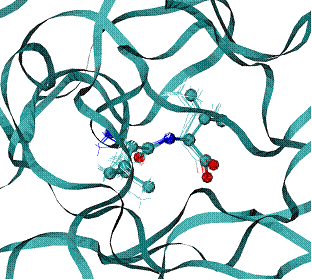
The best binding energy mode has RMSD = 0.46 A from the native binding mode of dipeptide ILE-VAL |
Table 1. Energies of top ranked binding modes, and RMSD from the native binding mode.
| Binding mode | ePL, kcal/mole | RMSD, A |
| Rank 1 -
LigDockFin001.001.pdb |
-76.07 | 0.46 |
| Rank2 -
LigDockFin001.002.pdb |
-75.6 | 0.58 |
| Rank3 -
LigDockFin001.002.pdb |
-75.5 | 0.78 |
| Rank4 -
LigDockFin004.001.pdb |
-74.8 | 0.88 |
Fig. 5. Human thrombin - 296 residues; MIT - molecule includes 80 atoms. |
A. Top Ranked calculated docking mode - red lines, CPK - native MIT in the native binding mode, RMSD = 0.2 A for calculated docking mode from the native.
|
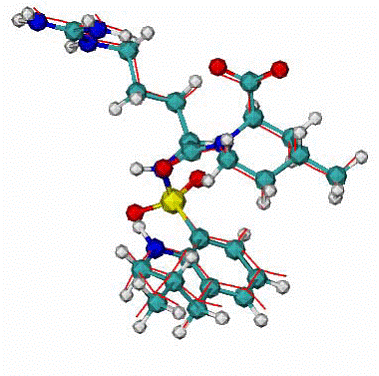 |
B. 1dwc complex. Red lines is docked MIT ligand, CPK is the native mode.
|
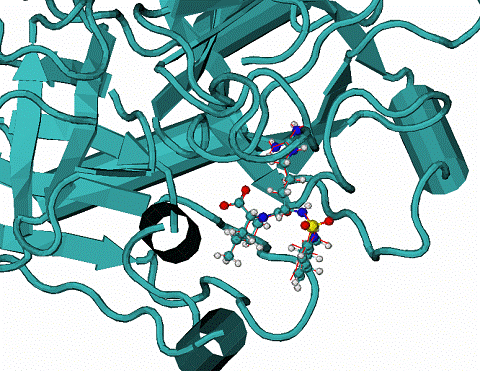
|
Fig.6. A. Two top ranked calculated binding modes of NOA in comparison with the NOA ligand in the native binding mode of 1hiv complex. CPK - native binding mode, lines (red and grey) the top ranked mode by energy of binding. The RMSD from the native are ~3.1 A for all atoms.
The major difference between native and calculated modes are the orientation of one aromatic double-ring at the top of molecule NOA, the RMSD = 1.1. A over all atoms except the later aromatic system.
|
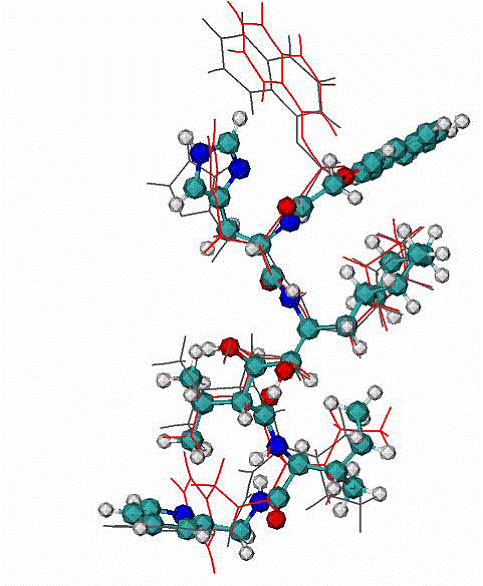 |
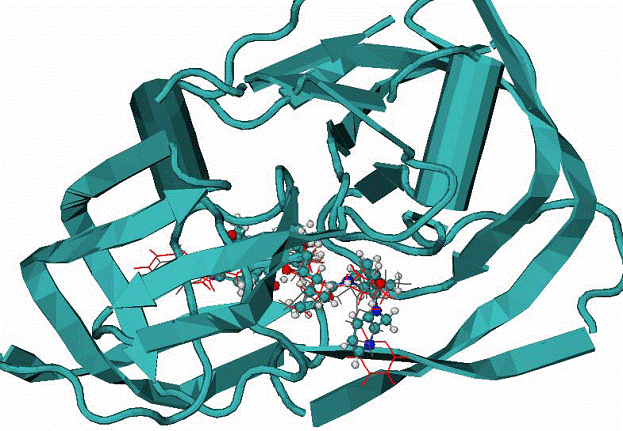
B. 1hiv complex of HIV1 protease with inhibitor NOA
CPK - native mode, red and grey lines - are calculated modes.
|
|
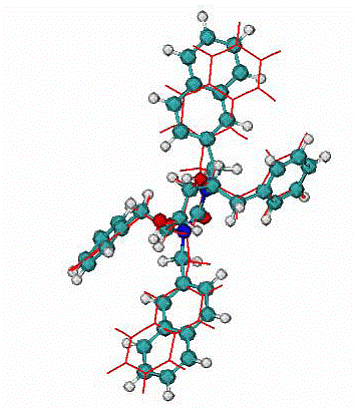
Fig. 7. A.
Calculated binding mode of XK2, red lines, CPK - native binding mode of XK2 ligand. RMSD = 0.95 A for all atom.
|
 |
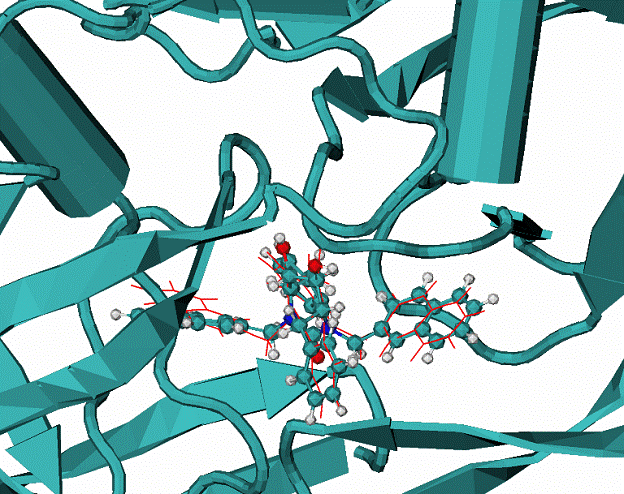
B.
Calculated docking mode for the ligand XK2 in complex with HIV1 protease, CPK - the native binding mode of the XK2 ligand.
|
|
Fig. 8. A.
Calculated best binding mode of VAC is in red lines, CPK - native VAC inhibitor in the 1hvp complex; the RMSD = 0.99 A.
|
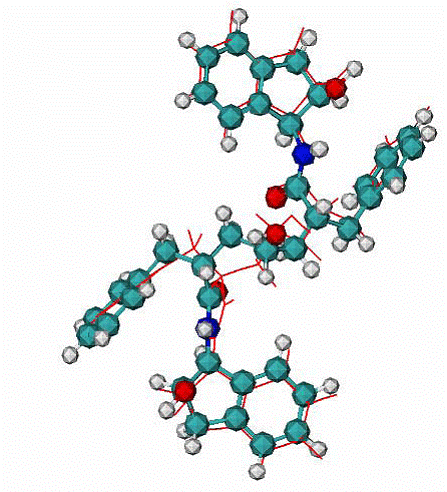 |
B. 4hvp complex, red lines is the calculated mode, CPK - the native binding mode of VAC inhibitor.
|
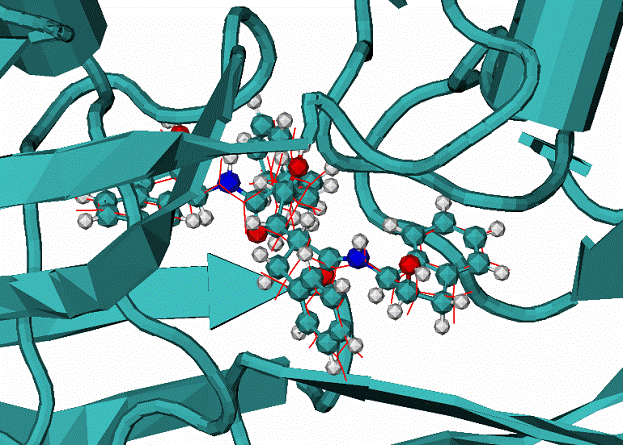
|
| Table 1. Results of MdDock method for a set of complexes | |||
| complex | Ntors | RMSD, A | DEgap |
| 1) 1bty trypsin/benz | 0 | 0.5 | 9.7 |
| 2) 1dwb a-thrombin/benz | 0 | 0.5 | 13.3 |
| 3) 1stp streptavidine/biotin | 5 | 0.96 | 29.5 |
| 4) 3tpi trypsinogen/Ile-Vla | 6 | 0.42 | 10.6 |
| 5) 1dwc a-thrombin/MIT | 8 | 0.2 | 10.8 |
| 6) 1hiv HIV1 protease/NOA | 16 | 1.1/3.1 | 2.6 |
| 7) 1hvr HIV1 protease/XK263 | 8 | 0.95 | 39.1 |
| 8) 4phv HIV1 protease/VAC | 15 | 0.9 | 3.4 |
Ntors - number of flexible torsion angles.
DEgap - energy gap between lowest energy binding mod and the next energy mode.
Conclusion:
The developed method of blind docking show a good accuracy in prediction of the native bindig modes of flexible ligands. At the test set of 8 ligands the method shows 100% accuracy, i.e. the native binding mode are found as the mode with highest binding energy calculated in the all-atom force field.
Tamar Schlick. Molecular Modeling and simulation. Springer-Verlag, New York, 2000.
Cornell W.D., Cieplak P., Bayly C.I., Gould I.R., Mertz K.M.,
Ferguson D., Spellmeyer D.C., Fox T., Caldwell J.W., Kollam P.A.
A second generation force field for the simulation of proteins, nucleic acids and organic molecules.
J.Am.Chem.Soc. 1995: 117, p.5179-5197
Lazaridis T., Karplus M. Proteins: Structu, Funct., and Gen. 1999: 35, p.133-152